Frequent Subgraph Mining

Order embedding

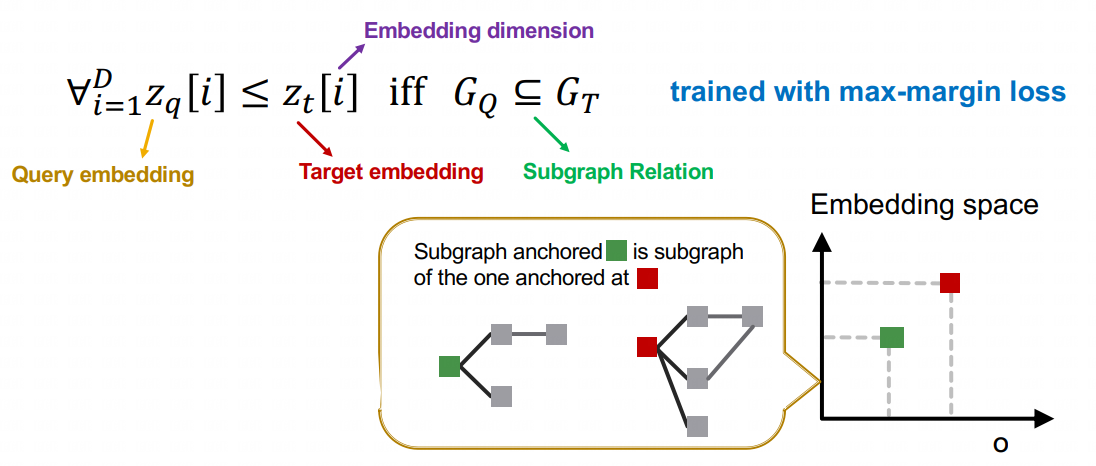
The purpose of order embedding is to encode two graphs, a query graph and a target graph, separately using Graph Neural Networks (GNNs). This is done by comparing the numerical values on each dimension of their embeddings in order to determine whether the two graphs have an isomorphic relationship.

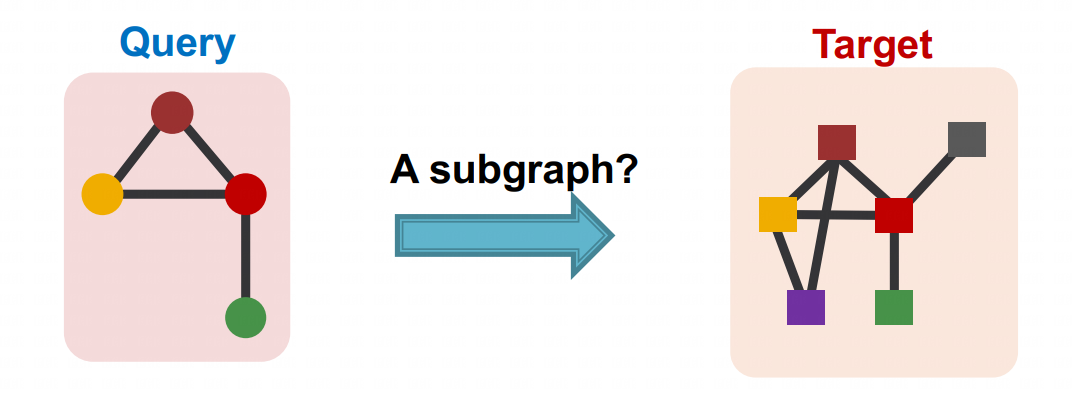
Neural Subgraph Matching

Subgraph isomorphism matching is one of the fundamental NP-complete problems in theoretical computer science, and applications arise in almost any situation where network modeling is done.

• In social science, subgraph analysis has played an important role in the analysis of network effects in social networks.
• Information retreival systems use subgraph structures in knowledge graphs for semantic summarization, analogy reasoning, and relationship prediction.
• In chemistry, subgraph matching is a robust and accurate method for determining similarity between chemical compounds.
• In biology, subgraph matching is of central importance in the analysis of protein-protein interaction networks, where identifying and predicting functional motifs is a primary tool for understanding biological mechanisms such as those underlying disease, aging, and medicine.

An efficient, accurate model for the subgraph matching problem could drive research in all of these domains, by providing insights into important substructures of these networks, which have traditionally been limited by either the quality of their approximate algorithms or the runtime of exact algorithms.

NeuroMatch treats the subgraph matching problem as a node identification problem: find node(s) in the target graph whose k-hop neighborhood contains the query. We separate this process has two parts: learning embeddings for the query and each target node, and then determining matches given the embeddings.

(1) As seen from the below figure, embeddings are learned via a GNN architecture, with one GNN applied to the target nodes (left) and one to the query nodes (right). (2) Given embeddings, we then use a simple rule for deciding whether a node is part of the subgraph: order embeddings . If every component of the embedding for the query is less than the corresponding component of the embedding for the target node, then we classify the target node's neighborhood as containing the query. We demonstrate the use of max margin loss to train the model in order to satisfy this order embedding constraint.

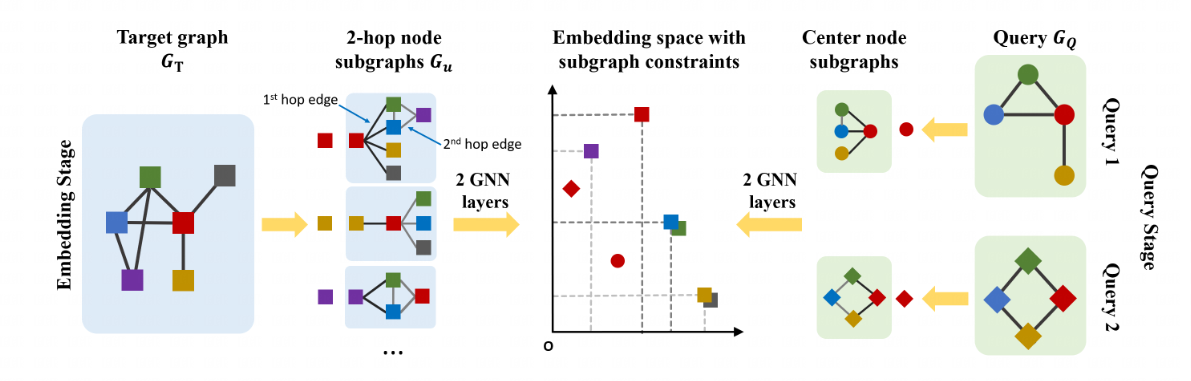
NeuroMatch features the following key techniques:

• Use of order embeddings constraints to improve accuracy and runtime performance.
• Optimization using node-anchored training objective, instead of learning graph-level embeddings.
• Pre-training subgraph matching on synthetic datasets and test / finetune on real datasets.
• Curriculum learning by feeding in more and more complex queries during training time. Runtime Efficiency. Oftentimes, we have a fixed set of target graphs that we want to run queries on. In this setting, NeuroMatch excels because the embeddings for nodes in the target graph can be precomputed and stored. As queries arrive, we need only run the embedding model on the small query graph and then compare the query embedding with the stored target embeddings to perform subgraph isomorphism matching. This facilitates inference time 100x faster than previous approaches, and 10x faster than the alternative to use a learned MLP to predict subgraph relationships.

SPminer

Finding subgraph patterns or network motifs that frequently recur in a graph dataset is important for identifying interpretable structural properties of complex networks. Example applications include:

• Biology: subgraph counting is highly predictive for disease pathways, gene interaction and connectomes
• Social science: subgraph patterns have been observed to be indicators of social balance and status
• Chemistry: common substructures are essential for predicting molecular properties

However, frequent subgraph mining has extremely high computational complexity. A traditional approach to motif mining is to enumerate all possible motifs Q of size up to k, usually up to 5, and then count appearances of Q in a given dataset. Frequent subgraph counting is very computationally challenging because it requires solving two intractable search problems:

1. Counting the frequency of a given motif Q in G.
2. Searching over all possible motifs Q to identify the frequent ones.

Problem (1) is NP-hard, while Problem (2) is also hard because the number of possible graphs Q increases super-exponentially with their size. SPMiner is the first neural approach to approximately identify the most frequent subgraphs, outperforming existing heuristics and search-based approximation algorithms.

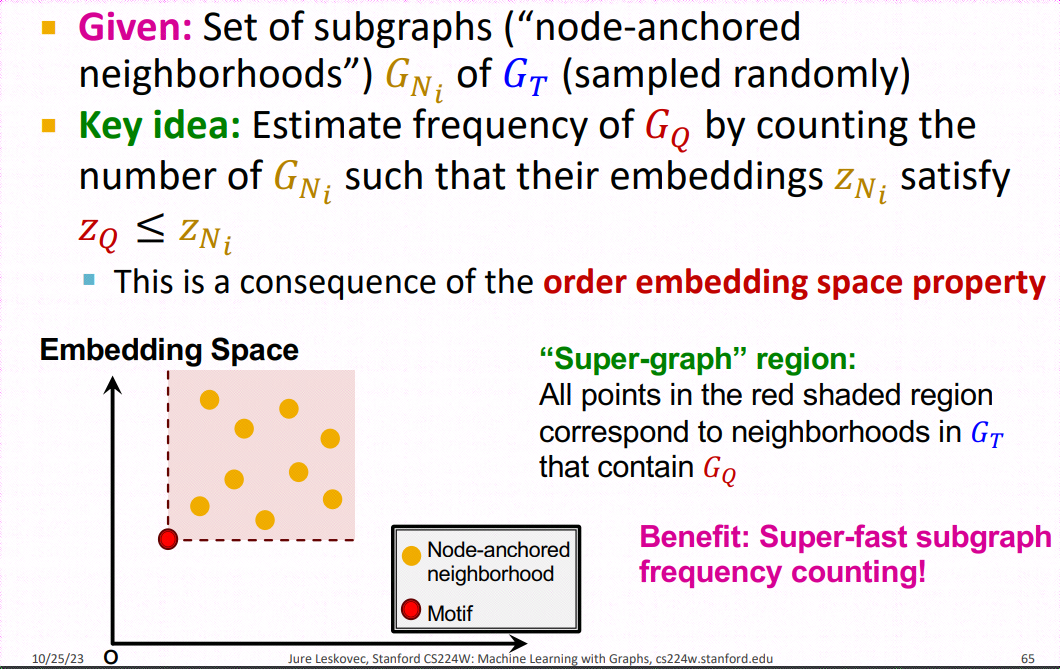
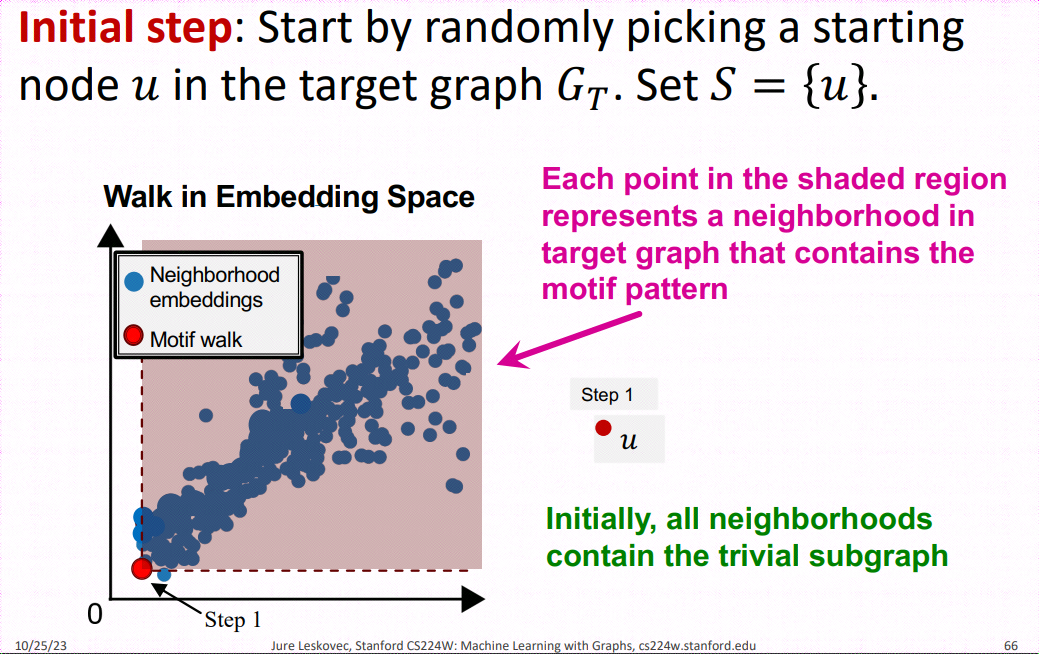
SP-Miner is a general framework using graph representation learning for identifying frequent motifs in a large target graph. It consists of two steps: an encoder for embedding subgraphs and a motif search procedure.

Encoder is an expressive graph neural network (GNN) with trainable dense skip layers. We decompose the input graph into overlapping node-anchored neighborhoods around each node. The encoder then maps these neighborhoods to points in an order embedding space. The order embedding space is trained to enforce the property that if one graph is a subgraph of another, then they are embedded to the "lower left" of each other (See part (a) for the figure above). Hence the order embedding space captures the partial ordering of graphs under the subgraph relation.

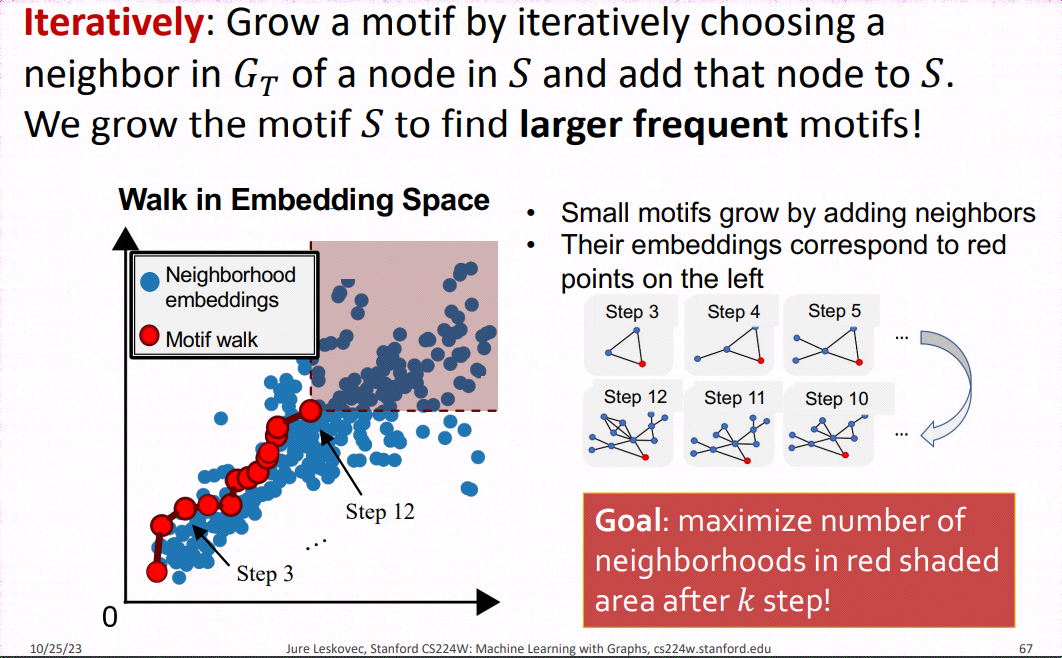
Motif Search Procedure SPMiner then reasons in the embedding space to identify frequent motifs of desired size k. SPMiner searches for a k-step walk in the embedding space that stays to the lower left of as many neighborhoods (blue dots) as possible (See part (b) of the figure above). The walk is performed by iteratively adding nodes and edges to the current motif candidate, and tracking its embedding. The number of subgraphs to the top right in the embedding space gives the frequency of the motif.

When the subgraph is expanded, it can be time-consuming to reevaluate each anchor in the space. Therefore, a common approach is to compute the number of subgraphs in the order embedding space and, during expansion, exclude isomorphic subgraphs in the neighborhood search that are eliminated by the current expansion, thereby speeding up the search process.