Hyperbolic Graph Neural Networks

Hyperbolic Graph Neural Networks (HGNNs) are a class of neural network models designed to handle data that exhibits hyperbolic geometry, which is particularly relevant for complex networks with hierarchical or non-Euclidean structures. These networks are inspired by the mathematical concept of hyperbolic spaces, which are non-flat spaces where the angles of a triangle can sum up to more than 180 degrees, unlike in Euclidean spaces.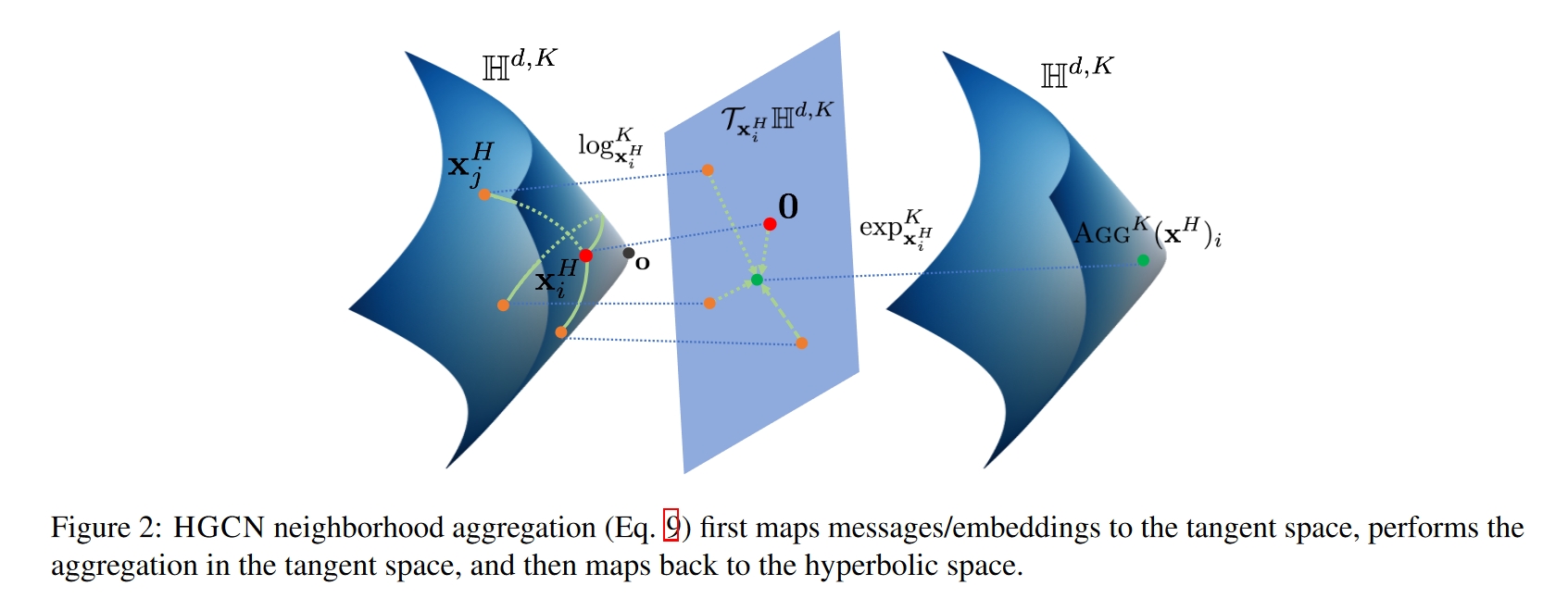

The approach of HGCN involves transforming graph data from Euclidean space to hyperbolic space, performing computations within the hyperbolic space, and then translating the results back into Euclidean space. This method allows for better utilization of the non-Euclidean characteristics of graphs.

Introduction

1. Motivation and Relevance: Many real-world networks, such as social networks, citation networks, and biological networks, exhibit hierarchical or non-Euclidean properties. Hyperbolic spaces provide a natural way to model these structures, as they can capture the notion of "closeness" in a way that reflects the network's inherent geometry.

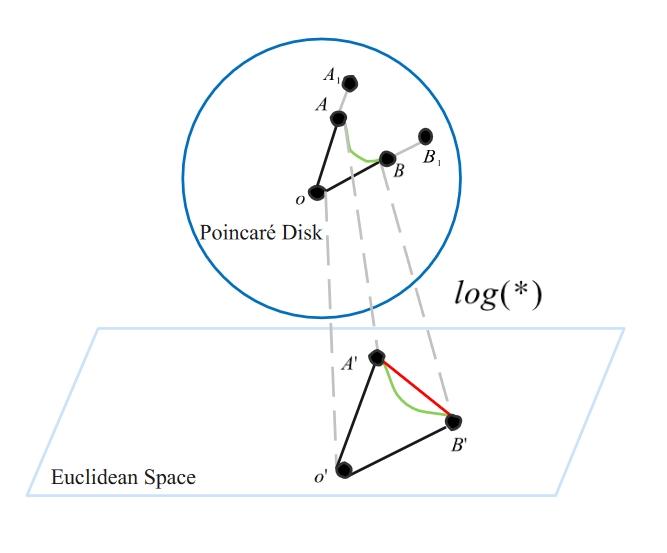
2. Hyperbolic Geometry: Hyperbolic spaces are characterized by their curvature, which is negative. This curvature allows for the representation of dense clusters and long-range connections, which are common in complex networks. The Poincaré disk model and the Poincaré half-space model are two common ways to embed hyperbolic spaces into Euclidean space for computational purposes.

3. Hyperbolic Embedding: HGNNs use hyperbolic embeddings to represent nodes in a network. These embeddings are learned during the training process and capture the hierarchical structure of the network. The embeddings are typically represented as points in a hyperbolic space, and the distances between these points reflect the network's structure.

4. Propagation Mechanism: HGNNs use a propagation mechanism that is adapted to the hyperbolic geometry. This mechanism allows information to flow between nodes in a way that respects the network's structure. The propagation can be thought of as a diffusion process, where information spreads from one node to its neighbors, but the distances and angles in the hyperbolic space influence how this information is updated.

5. Learning and Training: Training HGNNs involves optimizing the network's parameters to minimize a loss function that measures the difference between the predicted and actual node representations or labels. This is typically done using gradient descent or other optimization algorithms, with the gradients computed in the hyperbolic space.

Differences with GNN

Hyperbolic Graph Convolutional Networks (HGCNs) and Graph Convolutional Networks (GCNs) are both types of neural networks designed for processing graph-structured data, but they operate on different geometrical assumptions underlying the representation of nodes and edges in the graph.

• Geometric Assumption:

  • GCNs: These networks are based on Euclidean geometry where the underlying assumption is that nodes can be embedded in a linear space and interactions between nodes are modeled using Euclidean distances. GCNs are effective for graphs that can be naturally represented in Euclidean space, such as grids or tree-shaped graphs.
  • HGCNs: In contrast, HGCNs are designed to handle graphs that exhibit hyperbolic geometry, which is useful for capturing hierarchical structures and long-range dependencies that are common in complex networks like social networks, citation networks, and biological networks. HGCNs use hyperbolic embeddings to represent nodes, which can better capture the "closeness" of nodes that are far away in the network structure.

• Embedding:

  • GCNs: The features of nodes are aggregated from their immediate neighbors, typically using a weighted sum of features, where weights are determined by the adjacency matrix of the graph.
  • HGCNs: Nodes are embedded into a hyperbolic space using methods like the Poincaré disk or half-space model. Information propagation in HGCNs takes into account the hyperbolic distances between nodes, which allows for a more nuanced understanding of the graph's structure.

• Propagation Mechanism:

  • GCNs: The propagation of information is typically based on a linear convolution operation that updates node features by aggregating information from neighbors. This process is repeated over multiple layers to capture higher-order neighborhood information.
  • HGCNs: The propagation mechanism in HGCNs is adapted to the hyperbolic geometry. The information flow is designed to respect the hyperbolic distances, which can lead to different patterns of aggregation and flow of features compared to GCNs.